Solutions for Systems of Nonlinear Equations and Inequalities: Two Variables
Solutions to Try Its
1. and 2. 3. 4. Shade the area bounded by the two curves, above the quadratic and below the line.
Solutions to Odd-Numbered Exercises
1. A nonlinear system could be representative of two circles that overlap and intersect in two locations, hence two solutions. A nonlinear system could be representative of a parabola and a circle, where the vertex of the parabola meets the circle and the branches also intersect the circle, hence three solutions. 3. No. There does not need to be a feasible region. Consider a system that is bounded by two parallel lines. One inequality represents the region above the upper line; the other represents the region below the lower line. In this case, no points in the plane are located in both regions; hence there is no feasible region. 5. Choose any number between each solution and plug into and . If then there is profit. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. No Solutions Exist 29. No Solutions Exist 31. 33. 35. 37. 39. 41.
41.
 43.
43.
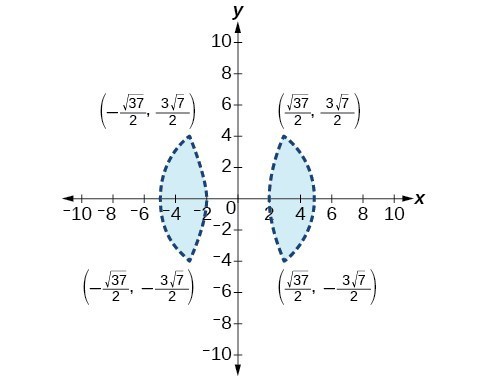 45.
45.
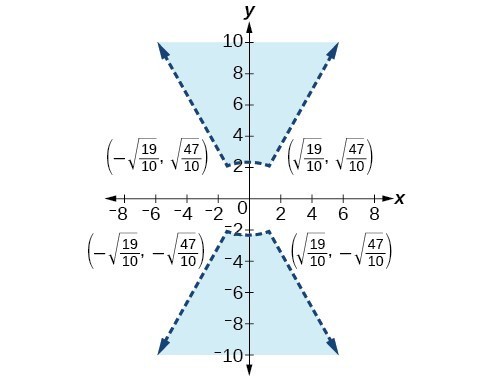 47.
47.
 49.
51. No Solution Exists
53. and
55. 12, 288
57. 2–20 computers
49.
51. No Solution Exists
53. and
55. 12, 288
57. 2–20 computers